育成の記録Vol.27

　

『土方カーブ』

　

皆さん、『土方カーブ』という言葉をご存知でしょうか？
計算式で『C²/8R』と表されるのですが初めて聞いたとき、数学好きな私は『アインシュタインの公式E=mc²』や『中学生の時に習ったπｒ²(パイアールジジョウ)』と同じくらい数学的響きがカッコよくて魅力を感じました。
今回のブログはいつもと志向を変え、計算式の美しさに魅了されてしまった『土方カーブ』についてご紹介させていただきます。

　

土方カーブとは？

　

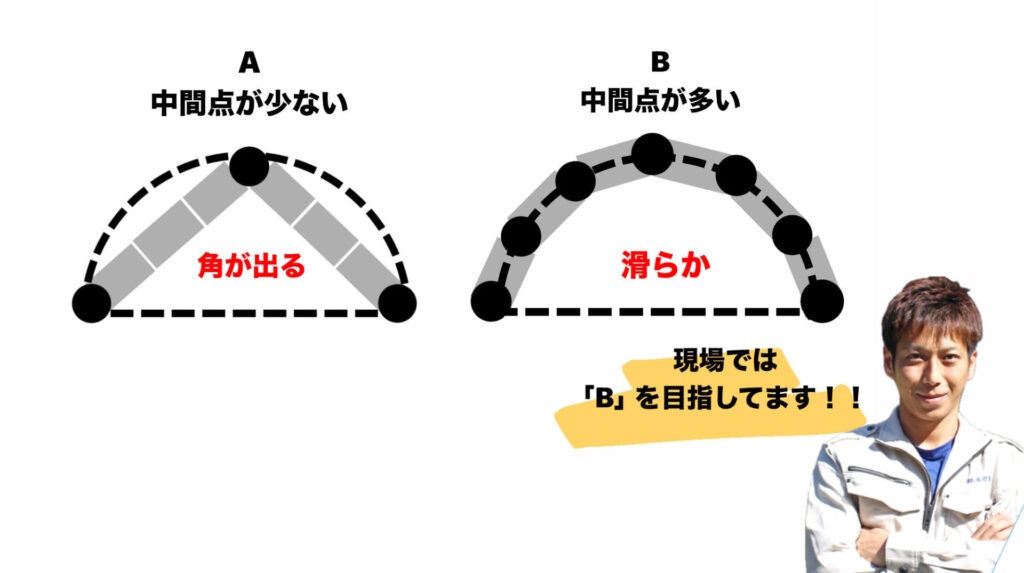
単カーブの測点と測点の中間点のポイントを簡単な計算で求める事ができる計算式の事です。
簡単にいうと、例えば側溝をカーブに沿って並べる際にこの計算式を使うことで、簡単にカーブ上にポイントを出す事が出来、カーブに沿った滑らかな敷設を行う事が出来るという事です。

　

　

土木カーブの計算式

　

といっても、カーブ上のポイントを出すなんて1回の計算では出ないでしょう？そう思われると思います。実際に、カーブ上のポイントを出そうと思うと、座標軸から落とすようになるので、ものすごい時間がかかりますが、この土木カーブを用いれば1回の計算で中間点のポイントを出す事が出来ます。

　

どうやって出すの？

　

ここからは図を用いてご紹介したいと思います。この図で紹介しているのは下記です。

【Ｒ】＝カーブの半径です。
【Ｃ】＝カーブ上に存在するA地点とB地点の直線距離です（弦長といいます）
【Ｌ】＝弦長から弧長までの距離（矢高といいます）
【Ｍ】＝土方カーブで出るポイント。C(弦長)の中心ポイントから垂直にＬ(矢高)を引いて弧長と重なる所

　

　

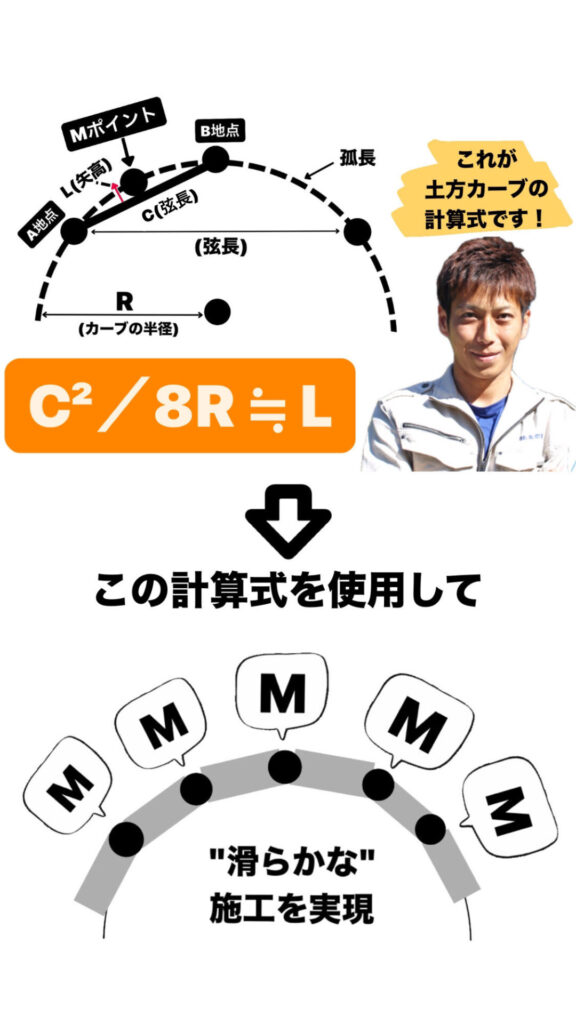
計算式は、C²/８Ｒ≒Ｌ

　

実践レポート

　

土方カーブについてをその後もYoutubeなどで学習していましたが、百聞は一見に如かずという事で実際に現場でも活用してみたところ、「そういうことか！」という発見もあり、更に感銘を受けました。

　

　

道に沿って側溝を入れる工程を行っている現場のポイント出しを行う際に実際に土木カーブを使って上記のＭのポイントを出してみました。写真はその時の様子です。側溝が滑らかなカーブを描けているのではと思います。

　

長田式　土方カーブ

　

一度、Mの値を出せば、その半分のM地点は、その前のM値を4で割ると出てくることも分かりました。
これを繰り返す事で更にキレイなＲを描く事が可能になります。